This and the next article talk about the a part of physics that plays the most direct role in creating the modern technology and life that we enjoy today - generating and using electricity.
This topic on electromagnetism is more about "using electricity". For "Generating electricity" will be explained in the next article on the topic of electromagnetic induction.
Many of us may have played with magnets at some stage. These are often small hard or flexible pieces ts that can attract an iron object.
Now if we wrap an electric wire a few times round an iron rod and pass an electric current through the wire, we would find that the iron rod can also attract the iron object!
In other words, the iron rod becomes a magnet! But if we then switch off the current, the iron object drops off. So without the current round the rod, the iron loses its magnetic property. This kind of "temporary" magnet is called an electromagnet.
So a magnet can somehow exert a force on iron objects near by. In earlier articles, we have seen that gravitational field and electric field have similar effects.
I have also described the method of using field lines to show directions and strengths of electric field around an electric charge. We can also do this for a magnet. It is called a magnetic field.
A long straight wire with an electric current through it produces a magnetic field around it the wire. The is a simple way to "see" the field lines - by sprinkling some iron filing (power) on a piece of paper around the wire. Like this.

You may just about see circular rings around the wire.
For a solenoid with an electric current, the field looks like this.

Notice the "lines" of iron powder inside the wire coil is roughly straight.
The quantity that tells us how strong a magnetic field is - is called magnetic flux density. It is usually represented by the letter B. We shall see later that this number can be used to calculate the force on a wire through the magnetic field - if the wire has an electric current.
There are formulae that we can use to calculate the magnetic flux density produced by electric current running through some simple wire shapes.
Long straight wire
Magnetic field at distance d from wire:
I is the electric current through the wire,
d is distance from the wire,
μ0 is a special number equal to 4π x 10-7 in SI units.
Flat circular coil
Magnetic field at centre of coil.
I is the electric current through the coil,
r is radius the coil,
N is the number of turns of coil.
Long solenoid
Magnetic field at centre of solenoid.
I is the electric current through the solenoid,
n is the number of turns for every 1 m length of the solenoid.
For typical electric currents we may get from a battery, the magnetic field produced by the above wire loops are relatively weak. For example, it may not pick up small iron nails are readily as a real magnet.
But there is a simple way to make this magnetic field a lot stronger - without have to increase the electric current. We just have to stick a piece of soft iron rod through the coil. But it is really the soft iron itself that gets magnetised and produces a strong magnetic field.
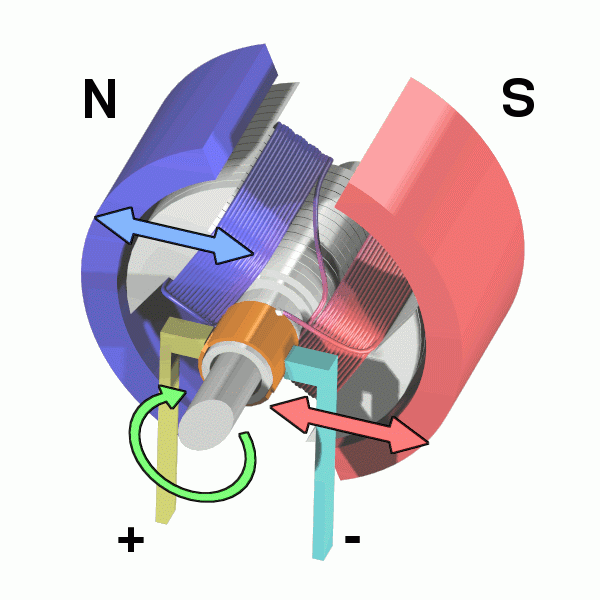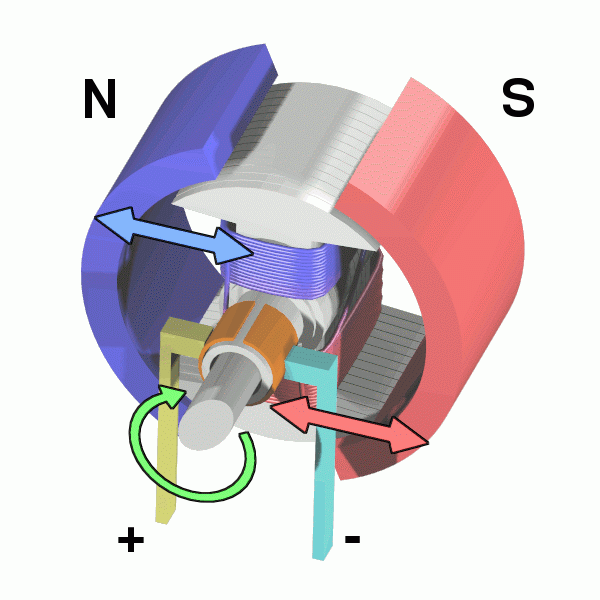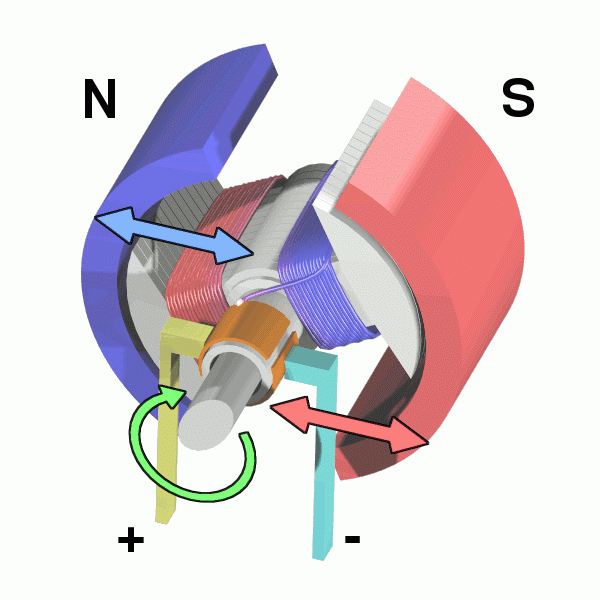
So we know that a wire carrying an electric current produces a magnetic field - just as a magnet would. What happens if we place this "current-carrying conductor" next to a magnet?
Answer: Just what we expect when you put a magnet next to another magnet. They would produce a force on each other.
For some simple setups, there may be simple formulae that we can use to calculate this force. One example is when we have a straight wire carrying an electric current, placed in a uniform magnetic field.
The force on a length of this wire is given by
L is the length of this wire
B is the magnetic flux density (how strong the field is) around the wire
I the electric current through the wire
θ the angle between the curremt and the magnetic field
In the special case when the angle θ is 90 degrees, the formula becomes simpler, just
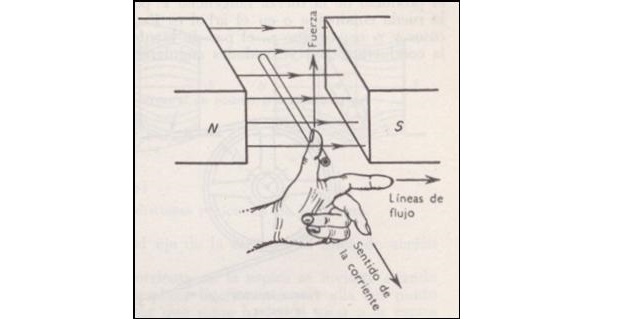
The formula above looks simple enough. It gives us the value of the force on the wire. But what direction is this force?
The formula above does not tell us. So we need another way to find out. This called "Fleming’s left hand rule". A picture is worth a thousand words. So here goes:
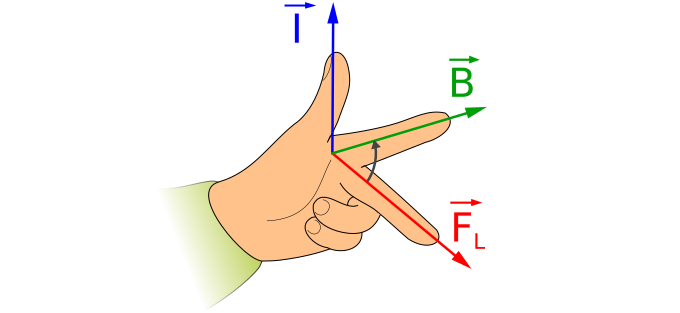
I can just imagine students stretching out their fingers and trying to figure out the direction of the force in an exam.
Lets look at the "B" in the formula above - the magnetic flux density. The formula just lets us calculate the force.
But what is "magnetic flux density"?
We know it has something to do with how strong the magnetic field is. We can guess that the bigger B is, the bigger is the force.
This is a common question in physics exam papers. The answer is obtained by rearranging the above equation when wire current and magnetic field are at right angle, like this:
Suppose that the is current 1 A and length of wire 1 m. Then magnetic flux density is
Equal to the force on the wire !
So the standard answer is :
"Magnetic flux density" is "the force acting per unit current per unit length on a wire placed at right angles to the magnetic field."
However, in my view, there is an issue with this answer. Magnetic flux density and force have different units. But this seems to be the standard way to define things now. So we have to remember when using this definition that quantities are assumed to be in SI units.
The formula
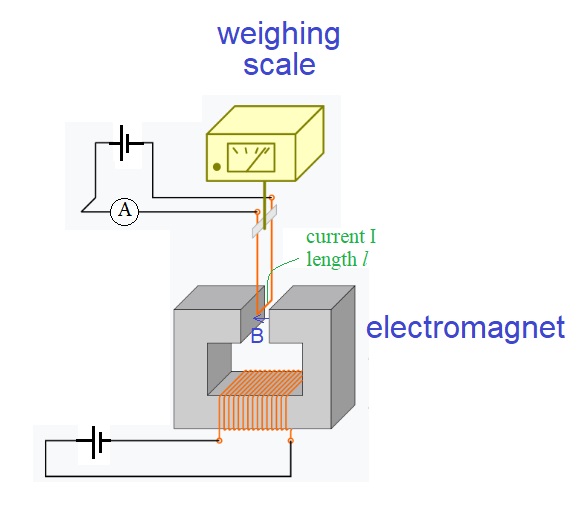
can be used to measure magnetic flux density. The way is to fix a wire of length L horizontally in a magnetic field that we want to measure. The magnet itself may be placed on a weighing scale. When switch on a current I through the wire, the wire will experience a force from the magnetic field.
But for every action, there is an equal and opposite reaction, according to Newton's third law. So the magnetic field generated by the wire's current would apply an equal and opposite force F on the magnet also. If we place this magnet on a weighing scale, the magnetic force would show as an increasing the weight on the weighing scale!
In this way, we can find F. Then we can use the formula above to calculate B.
This setup is called a current balance, and is a method to measure the flux density of a magnetic field. There is more than one way to set up this measurement. Here is an example.
We can use the ideas above to predict the direction of forces between two parallel wires that have electric currents flowing in the same direction. Do you think they would attract or repel?
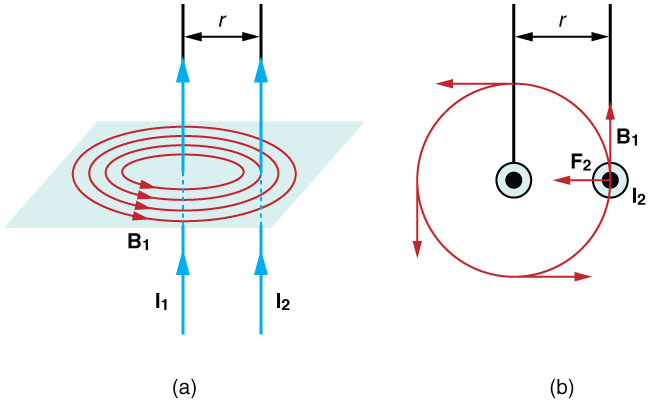
Answer: Attract !
Around 1900, scientists found that if you connect two metal plates in a vacuum tube to a high voltage, electric current can go through the vacuum!
What is a vacuum? A vacuum is nothing. Really nothing. Not even air - or maybe just very very little air. Surely, an electric current needs a conductor to go through!
Today, we learn in school physics that these scientists went on to discover electrons, and finally understood that electric current flowing in a circuit is really electrons flowing flowing through there wires.
Not only that. They actually put this into our physics syllabus! So instead of finishing here, I have to go on writing a bit more.
So the scientists tried many things to find out what is going on. And one of the experiments that really helped with their understanding looked at bit like this.
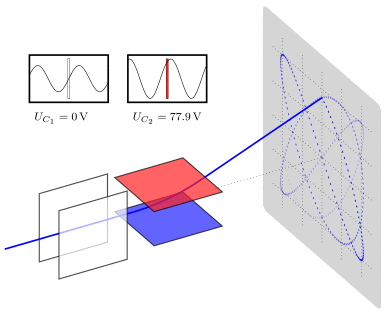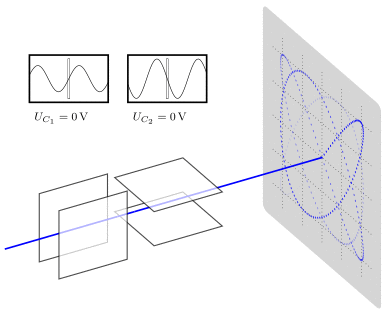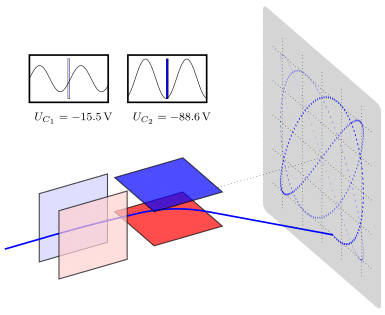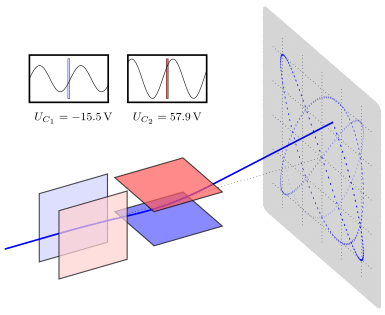
After many years of experiments, they finally understood that what is jumping through the vacuum are tiny particles with negative charge. Today, we call them electrons.
At first, they could only do simple experiments. They let the particles go through a small hole. Then they put an electric field or magnetic field next to the vacuum tube and see how the particles change direction. Eventually, they were able to measure something called the charge to mass ratio of the electron.
"Charge to mass ratio" here just means the value you get if you when you divide the charge of the electron by its mass. But what is the mass and what is the charge?? Well, that would have to wait until Millikan did his oil drop experiment some years later.
I have actually gone on a small detour to provide some background history, so that the last part of this syllabus makes more sense. The last part is about using this magnetic force to find the velocity of a charged particle.
Recall from the above that the force F on a wire carrying an electric current I in a magnetic field B is given by
We now learn that there is also a force on a single particle with an electric charge q and a velocity v, going through a magnetic field B at an angle θ to the field. This force is given by :
If the particle is moving at right angle to the magnetic field, then this formula becomes simpler:
This magnetic force pulls the particle in one direction. So how can this be used to find the "charge to mass ratio"?
It is actually quite simple. Just apply an electric field to pull the particle back, so that it goes straight again!
To see why this works, notice from the two formulae above that if magnetic and electric force are equal, then
So we can just divide E by B and get the particle velocity!

You can learn these concepts and more at Dr Hock's maths and physics tuition.